In the book Missing Billionaires, Victor Haghani and James White argue that through the power of compound interest, there should be many more billionaires around – simply through time, even with modest investment performance. The reason why there are “missing” billionaires is not because they didn’t find the optimal asset allocation, it’s due to making poor risk decisions and/or excessive spending (and then taking big risks to keep the fun times rolling).
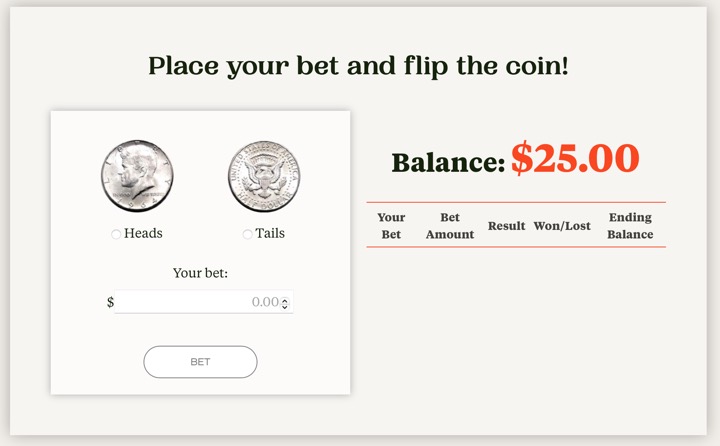
For example, one simple way that you can lose money even with the odds in your favor is poor bet sizing. The authors created the Elm Wealth Coin Flip Challenge in order to teach this interactively. In the game, the coin is altered such that you know it will come up heads 60% of the time, and tails 40% of the time. If you know anything about gambling in the real world, you’ll know this is a huge advantage! Dramatic movies about card counting and the MIT Blackjack team involves edges of only ~1%.
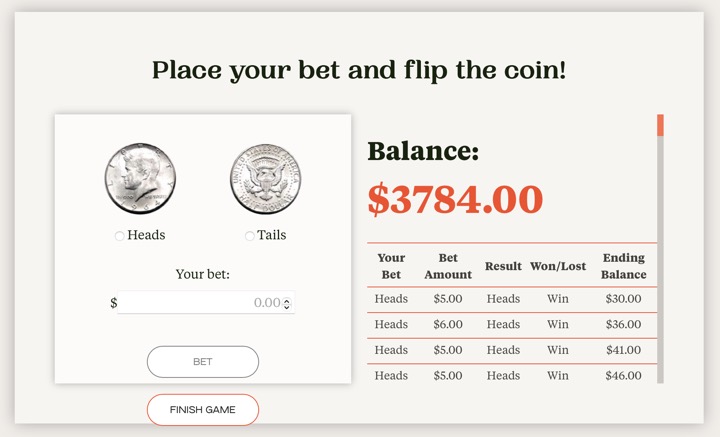
You get $25 to wager, and you can bet any amount you have. Can you build your stack up to thousands of dollars? Try for yourself, first with just your intuition. You’ll soon discover that it’s harder than it looks! Too little a bet, and the needle doesn’t really move much even on the good swings. Too big a bet, and you can’t survive the bad swings. It’s quite easy to dwindle quickly down to zero. After that, as Warren Buffett has stated, “Anything times zero is zero.”
Nowadays, we all have a 24/7 casino lurking in our pockets. With ads constantly telling us we can get rich with crypto, stock options, and sports betting, I think it’s very critical to teach ourselves and our kids about these concepts like odds and betting. Warren Buffett once bought and installed slot machines in his own house, to teach his kids about the one-armed bandits. Investing done right with proper risk management is a positive-sum game with excellent odds for the investor. Crypto speculation, aggressive use of stock options, and sport betting are only excellent for the “house” and I fear will create a generation of missing wealth. The next wave of volatility will come soon enough.
The Best Credit Card Bonus Offers – 2025
Big List of Free Stocks from Brokerage Apps
Best Interest Rates on Cash - 2025
Free Credit Scores x 3 + Free Credit Monitoring
Best No Fee 0% APR Balance Transfer Offers
Little-Known Cellular Data Plans That Can Save Big Money
How To Haggle Your Cable or Direct TV Bill
Big List of Free Consumer Data Reports (Credit, Rent, Work)
This is interesting but is there a good takeaway from it? For example, with investable assets of $X you should consider a bet in the $Y-Z range when the risk is P%? Would this provide more information beyond the ratios of your 2-3 fund portfolio of low cost index funds for the Bogleheads?
The classic Kelly formula is designed for a simple binary outcome (win or lose). The recommended wager, as a fraction of your current bankroll, is: \(f*=\frac{pb-q}{b}\) Where: \(f*\) is the fraction of the current bankroll to bet.\(p\) is the probability of winning.\(q\) is the probability of losing, which equals \(1-p\).\(b\) is the decimal odds, minus one. In other words, it’s the payoff you get for a one-unit wager. For a bet with even money odds (+100 or 2.0), \(b=1\).
Example calculation Imagine a rigged coin with a 60% chance of landing on heads. You are offered an even-money payout, meaning if you bet $100 and win, you get your $100 back plus another $100 in profit. \(p\) = 0.60\(q\) = \(1-0.60=0.40\)\(b\) = 1 (even money) The calculation is: \(f*=\frac{(0.60)(1)-0.40}{1}=\frac{0.60-0.40}{1}=0.20\) The formula advises betting 20% of your bankroll on heads.
60% heads and 40% tails. Hmmmm. Sounds like the old 60% stock/ 40% bond allocation recommendation. The book sounds interesting. Considering how many individuals with average incomes somehow manage to leave estates worth several millions, there should probably also be many more millionaires, too?